下面我们讨论另外一个优化技术。

如前所述，比特币的数据库大小已经超过140GB，由于天生的去中心化特性，比特币网络中的每个节点都是独立、自立的，这意味着每个节点必须存储整个blockchain。随着比特币使用者的日益增多，人人拥有整个blockchain变得越来越困难。同时，作为完全的参与者，富有对交易和block进行验证的责任，这需要节点之间通过网络进行交互从而下载新的block。

在中本聪发布的比特币白皮书中，针对此问题提供了一个解决方案：SPV（Simplified Payment Verification）。SPV是一个轻量级的比特币节点，该节点不会下载整个blockchain，也不会对block和交易进行验证，而是通过查找block中的交易来验证支付，同时连接到一个完整节点获取所需数据。SPV机制允许多个轻量级节点对应一个完整节点。为了实现SPV，需要一种交易检测方法，若包含该交易就无需下载整个block，此时默克尔树派上用场了。

比特币使用默克尔树获取交易hash值，交易hash值保存在block的头信息中，应用于PoW。目前，仅仅将一个block中所有交易的hash值简单地组合在一起，然后再使用SHA256算法生成hash值，虽然这也可以为block的交易集合创建唯一标识，但默克尔树有一些额外的优势。

默克尔树如下所示：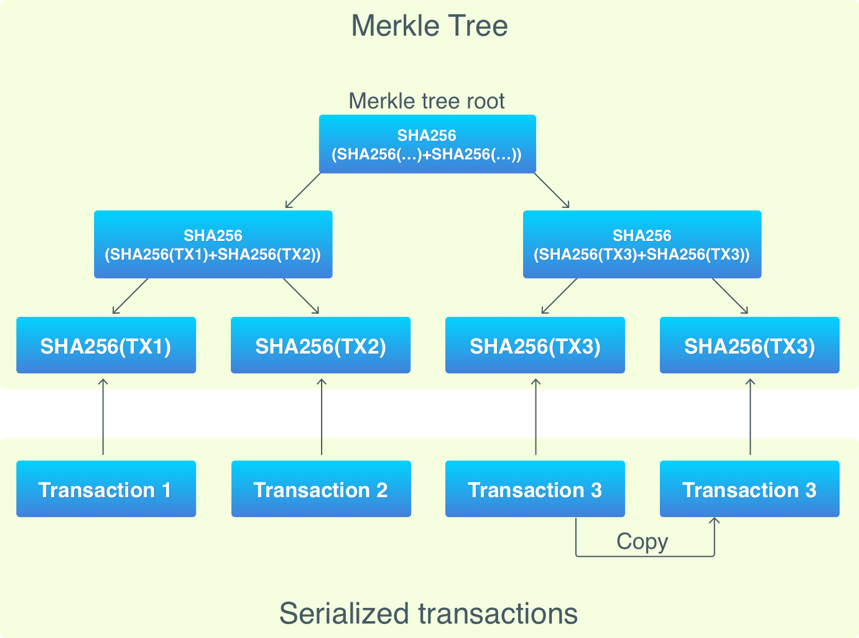
每个block有一个默克尔树，树中每个叶子节点是一个交易的hash值（比特币使用双重SHA256哈希）。叶子节点的数量一定是偶数，然后并非每个block都恰好有偶数个交易。当block有奇数个交易时，最后一个交易会被复制一次（复制仅仅发生在默克尔树中而不是block中！）。

默克尔树自下而上的进行组织，叶子节点成对分组后将两个hash值组合后生成新的hash值，形成上层的树节点，重复整个过程直到只有一个树节点为止，也就是所说的根节点。根节点的hash值是整个交易集的唯一标识，保存在block头信息中，用于PoW过程。

默克尔树的好处是：验证某个交易不需要现在整个block，而仅仅需要交易hash值、默克尔树根节点hash值以及默克尔路径即可。

下面让我们开始写代码：

type MerkleTree struct {
    RootNode *MerkleNode
}

type MerkleNode struct {
    Left  *MerkleNode
    Right *MerkleNode
    Data  []byte
}

func NewMerkleNode(left, right *MerkleNode, data []byte) *MerkleNode {
    mNode := MerkleNode{}

    if left == nil && right == nil {
        hash := sha256.Sum256(data)
        mNode.Data = hash[:]
    } else {
        prevHashes := append(left.Data, right.Data...)
        hash := sha256.Sum256(prevHashes)
        mNode.Data = hash[:]
    }

    mNode.Left = left
    mNode.Right = right

    return &mNode
}

NewMerkleNode方法用于创建MerkleNode：当节点为叶子节点时，Data保存某个交易的hash值；当节点为非叶子节点时，Data保存两个子节点生成的hash值。

func NewMerkleTree(data [][]byte) *MerkleTree {
    var nodes []MerkleNode

    if len(data)%2 != 0 {
        data = append(data, data[len(data)-1])
    }

    for _, datum := range data {
        node := NewMerkleNode(nil, nil, datum)
        nodes = append(nodes, *node)
    }

    for i := 0; i < len(data)/2; i++ {
        var newLevel []MerkleNode

        for j := 0; j < len(nodes); j += 2 {
            node := NewMerkleNode(&nodes[j], &nodes[j+1], nil)
            newLevel = append(newLevel, *node)
        }

        nodes = newLevel
    }

    mTree := MerkleTree{&nodes[0]}

    return &mTree
}

创建一个默克尔树之前，需要确保有偶数个叶子节点，然后将数据转换为叶子节点，最后生成整个默克尔树。

译者注：上述实现存在一个问题：当叶子节点的数量是2n时，可以正常创建树（for j := 0; j < len(nodes); j += 2…该段代码体现）；如果是不是2n时，创建树会发生异常！

修改Block.HashTransactions方法，用于获取在PoW过程获取交易hash值。

func (b *Block) HashTransactions() []byte {
    var transactions [][]byte

    for _, tx := range b.Transactions {
        transactions = append(transactions, tx.Serialize())
    }
    mTree := NewMerkleTree(transactions)

    return mTree.RootNode.Data
}